Es un interesante problema que debería de explicarse cuando apenas nos adentramos al estudio de la teoría de grafos, ya que en si este problema refleja la importancia de dicho campo, como se van modelando problemas del mundo real como graficas y a su vez conocer el concepto de un ciclo Euleriano. Este problema da inicio a la teoría de grafos.
El problema dice lo siguiente:
Dado el mapa de Königsberg, con el río Pregolya dividiendo el plano en cuatro regiones distintas, que están unidas a través de los siete puentes, ¿es posible dar un paseo comenzando desde cualquiera de estas regiones, de modo de recorrerlas todas pasando sólo una vez por cada puente, y regresando al mismo punto de origen?

Imaginemos si lo intentáramos resolver mediante fuerza bruta, intentando cada una de las posibilidades hasta el cansancio, obviamente sin llegar al resultado esperado :P
Leonhard Euler un matemático en el año 1736 propone una ingeniosa y a la vez sencilla, forma de solucionar el problema, no solo para este caso, si no para muchos más que pueden diferir en la cantidad de puentes.
Euler formuló el problema de la siguiente manera: “En la ciudad de Königsberg, en Prusia, hay una isla llamada Kneiphof, rodeada por los dos brazos del río Pregel. Hay siete puentes a, b, c, d, e, f y g, que cruzan por los dos brazos del río. La cuestión consiste en determinar si una persona puede realizar un paseo de tal forma que cruce cada uno de estos puentes sólo una vez”.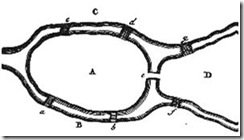
Euler primeramente realizo una abstracción del modelo del mapa, quedando de una manera mucho más simple en donde él representa con puntos las regiones y con líneas los puentes que hay entre punto a punto. De esta forma el problema se reduce considerablemente.
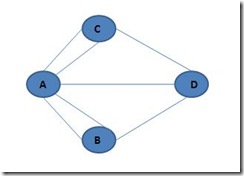
Como resultado de ello Euler llego a la conclusión que no existe un camino, en el que pueda recorrer toda la ciudad solo pasando una sola vez.
Pero como sabemos los matemáticos son bastante analíticos, Euler no se conformo con dejarlo así, si no que nos dio una explicación razonable.
Según Euler, todo se basaba en utilizar una notación adecuada.
Entonces , Euler llamó A, B, C y D a las distintas regiones de Königsberg. El camino que va desde A hasta B puede ser por el puente a o por el b, pero Euler lo designó por AB. Una vez allí, para ir a D, se sigue el camino BD, designando la trayectoria total por ABD, y así sucesivamente hasta recorrer todas las zonas y puentes, de manera que al final se obtendrá una combinación de ocho letras. Sin embargo esta notación tiene un inconveniente, y es que no tiene en cuenta que para ir de una zona a otra puede que exista más de un puente.
Euler vio que esta situación concreta no era posible, ya que, por ejemplo, si se empieza en la región A, si esta región sólo conectara con el puente a, como puede que se llegue o se venga de ella, la letra A aparecería una vez en la combinación de 8 letras. Si hubiera tres puentes que condujeran a la zona, entonces la letra A aparecería dos veces. Pero como llegan cinco puentes, en este caso, A debe aparecer tres veces en esa sucesión. Similarmente, B estaría dos veces; al igual que D y C. Pero entonces, ya tendríamos nueve letras en la sucesión, cuando para ser la ruta posible únicamente deberían haber ocho. Euler dedujo entonces que no se podía realizar la travesía requerida a través de los siete puentes de Königsberg .
Sin embargo, y como comente anteriormente, Euler no se contentó sólo con solucionar esta situación concreta, sino que se dedicó por completo al estudio del problema en general, obteniendo una solución que servía también para cualquier número de puentes.
Para ello, el procedimiento que siguió Euler consistió en lo siguiente: en primer lugar, apuntó en un papel el número de puentes más uno (ocho, en el caso de Königsberg ). Después, abajo a la izquierda formó una columna con todas las letras de las regiones (A, B, C y D, en este caso). A su derecha, formó una segunda columna con el número de puentes que salen de cada una de las correspondientes zonas (5, 3, 3 y 3, en este caso), marcando con un asterisco aquellas letras de las que salen un número par de puentes.
Después realizó las siguientes operaciones con los números de la segunda columna: si el número de la segunda columna (número de puentes que llegan a una determinada región) es impar, lo sumo en una unidad y lo dividió entre dos. Si el número es par, lo dividió entre dos. Euler colocó finalmente a la derecha una tercera columna con las cuentas anteriormente especificadas (3, 2,2, 2, en nuestro caso).
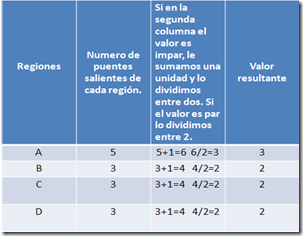
Euler entonces llego a la conclusión que el problema sólo tendría solución si la suma de los números de la última columna es menor o igual al numero de puentes sumando una unidad. En este caso 7 puentes sumando 1 dando lugar a 8. Ese debería de ser la sumatoria de la ultima columna en dado caso que existiera una solución. En nuestro caso la sumatoria es igual a 9 es por ello que Euler determino que no existe una solución para el problema de los puentes de Königsberg
Para comprender mucho mejor la manera en que Euler resolvio el problema, es importante apreciar las siguientes cuestiones:
•La suma de los números de la segunda columna, es siempre par, ya que su mitad refleja el número de puentes.
• Si la suma de dichos números se aumenta en dos unidades y luego se divide entre dos, el resultado es el número escrito en la parte superior de la tabla construida.
• Si los números de la segunda columna son todos pares, la tercera columna, formada por las mitades de ellos, sumará una unidad menor que el número escrito inicialmente de la tabla (con lo que la ruta será siempre posible)
• Si en la segunda columna hay sólo dos números impares, la ruta requerida será también siempre posible, porque la suma de la tercera columna coincidirá con el número inicial.
• Si hay más de dos números impares en la segunda columna,la ruta no será nunca posible, pues la suma de la tercera columna superará siempre al número inicialmente escrito.
Entonces Euler dedujo algunas reglas para cruzar todos los puentes una sola
vez, se tienen que cumplir las siguientes condiciones:
• Si hay más de dos regiones a las que conducen un número impar de puentes, la ruta no será posible.
• Si sólo hay dos regiones a las que llega un número impar de puentes, la ruta se podrá realizar, comenzando en una de esas regiones.
• Si no hay regiones a las que conduzcan un número impar de puentes, la ruta pedida se podrá realizar, comenzando en cualquier punto.
Con esto Euler dio inicio a las primeras nociones de un grafo, donde el modeló el problema de los 7 puentes como un grafo, los vértices representaban cada una de las regiones y las aristas las conexiones entre ellas.
Con la demostración de Euler, también surgió lo que conocemos en teoría de graficas como ciclo euleriano, llamado así justamente en honor a Leonhard Euler, que representa cualquier camino dentro de un grafo particular, capaz de recorrer todas las aristas una única vez, regresando finalmente al mismo vértice original.
Referencias recomendadas:
http://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg
http://mathforum.org/isaac/problems/bridges1.html
http://en.wikipedia.org/wiki/Eulerian_path
http://www.iesezequielgonzalez.com/matematicas/grafos.htm
http://es.wikipedia.org/wiki/Problema_de_los_puentes_de_K%C3%B6nigsberg
http://es.wikipedia.org/wiki/Ciclo_euleriano

<3 +4
ResponderEliminar